Hubungan antara Unsur-Unsur Bangun Ruang
Hubungan antara Unsur-Unsur Bangun Ruang - Tentu kalian masih ingat dengan macam-macam bangun ruang bukan?
Apakah kalian masih ingat dengan definisi titik, garis, dan bidang?.

✍ Garis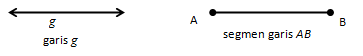
✍ Bidang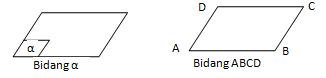
Nah, sekarang kalian sudah ingat kembali mengenai definisi titik, garis, dan bidang bukan?
✿ Titik dikatakan terletak pada garis jika garis melalui titik .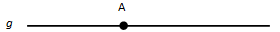

Berdasarkan hubungan di atas, tahukah kalian bagaimana cara menentukan proyeksi titik pada garis dan jarak titik ke garis?
☞ Proyeksi Titik pada Garis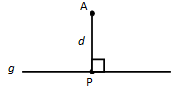
☞ Jarak Titik ke Garis
✿ Titik dikatakan terletak pada bidang jika bidang melalui titik .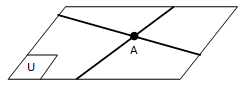
Berdasarkan hubungan di atas, tahukah kalian bagaimana cara menentukan proyeksi titik pada bidang dan jarak titik ke bidang?
☞ Proyeksi Titik pada Bidang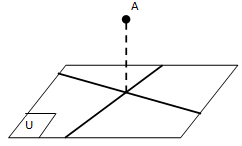
☞ Jarak Titik ke Bidang
✿ Dua Garis Berimpit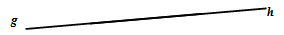
✿ Dua Garis Sejajar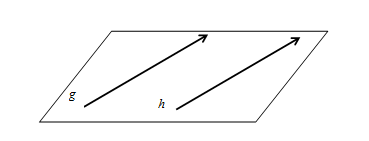
✿ Dua Garis Berpotongan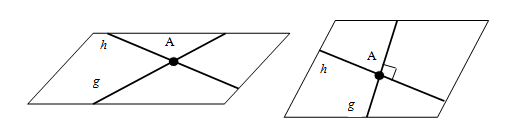
✿ Dua Garis Bersilangan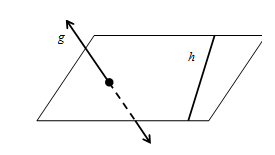
✿ Garis Terletak pada Bidang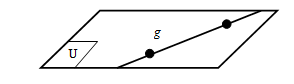
✿ Garis Sejajar Bidang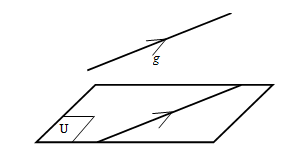
✿ Garis Menembus/Memotong Bidang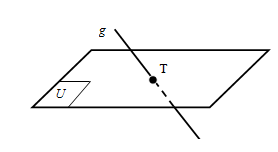
Apakah kalian sudah paham dengan penjelasan di atas?
✿ Dua Bidang Berimpit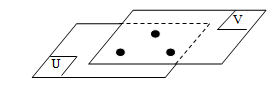
✿ Dua Bidang Sejajar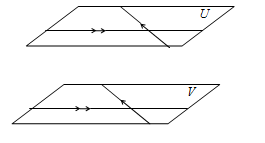
✿ Dua Bidang Berpotongan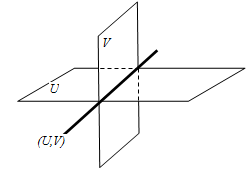
Agar kalian lebih paham mengenai materi di atas, yuk kita perhatikan contoh berikut.
Penyelesaian:
Perhatikan kubus berikut.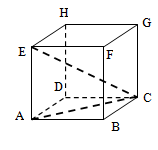
 |
| Hubungan antara Unsur-Unsur Bangun Ruang |
Bangun ruang seperti kubus, balok, limas, prisma, kerucut, tabung, dan bola masing-masing memiliki beberapa unsur, yaitu sisi, rusuk, titik sudut, diagonal sisi, diagonal ruang, dan bidang diagonal.
Nah, dalam topik kali ini kalian akan belajar tentang hubungan antara unsur-unsur pada bangun ruang, meliputi hubungan antara titik, garis, dan bidang.
Apakah kalian masih ingat dengan definisi titik, garis, dan bidang?.
Yuk kita ingat kembali.
Konsep Dasar
✍ Titik
Suatu titik ditentukan olah letaknya dan tidak memiliki besaran (tidak berdimensi).

Suatu titik digambarkan dengan noktah dan dinotasikan dengan huruf kapital, seperti , , , dan seterusnya.
✍ Garis
Garis merupakan himpunan titik-titik yang banyaknya tidak terbatas.
Suatu garis (garis lurus) hanya memiliki panjang dan tidak memiliki lebar, sehingga garis dikatakan berdimensi satu.
Suatu bagian garis yang terbatas dan mempunyai ujung dan pangkal dinamakan dengan segmen garis (ruas garis).
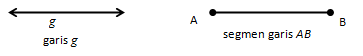
Garis biasanya dinotasikan dengan huruf kecil atau segmen garis dari titik pangkal ke titik ujung seperti , , , atau segmen garis , , dan seterusnya.
✍ Bidang
Suatu bidang (bidang datar) mempunyai luas yang tak terbatas. Namun, untuk memudahkan dalam menggambarkannya, kita hanya menggambarkan sebagian bidang saja, yang disebut dengan wakil bidang.
Bidang dikatakan berdimensi dua, sebab suatu bidang memiliki panjang dan lebar.
Bidang dinotasikan dengan simbol seperti , , atau titik-titik sudut bidang tersebut.
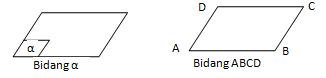
Nah, pada bangun ruang bidang datar, bidang-bidang pembentuknya adalah bidang datar, sedangkan pada bangun ruang sisi lengkung, bidang sisinya berbentuk bidang lengkung.
Nah, sekarang kalian sudah ingat kembali mengenai definisi titik, garis, dan bidang bukan?
Yuk kita cermati hubungan antara dua titik dalam uraian berikut.
Hubungan antara Dua Titik
Hubungan yang mungkin terbentuk dari dua buah titik adalah berimpit atau tidak berimpit.
- Dua titik dikatakan berimpit jika kedua titik tersebut memiliki koordinat yang sama.
- Dua titik dikatakan tidak berimpit jika kedua titik tersebut tidak memiliki koordinat yang sama.
Hubungan antara Titik dan Garis
Ada dua hubungan yang mungkin terjadi, yaitu titik terletak pada garis atau titik terletak di luar garis.
✿ Titik dikatakan terletak pada garis jika garis melalui titik .
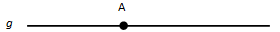
✿ Titik dikatakan terletak di luar garis jika garis tidak melalui titik .

Berdasarkan hubungan di atas, tahukah kalian bagaimana cara menentukan proyeksi titik pada garis dan jarak titik ke garis?
Yuk kita temukan jawabannya dengan mencermati ilustrasi berikut.
☞ Proyeksi Titik pada Garis

Untuk menentukan proyeksi titik pada garis , kita perlu menentukan titik pada garis sedemikian hingga garis tegak lurus dengan garis .
Nah, titik tersebut adalah proyeksi titik pada garis .
☞ Jarak Titik ke Garis
Pada gambar di atas, jarak antara titik pada garis sama dengan panjang garis , yaitu satuan.
Hubungan antara Titik dan Bidang
Sebuah titik dapat terletak pada bidang atau berada di luar bidang.
✿ Titik dikatakan terletak pada bidang jika bidang melalui titik .

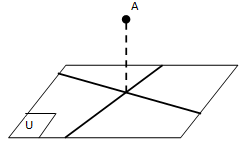
✿ Titik dikatakan berada di luar bidang jika bidang tidak melalui titik .

Berdasarkan hubungan di atas, tahukah kalian bagaimana cara menentukan proyeksi titik pada bidang dan jarak titik ke bidang?
Yuk kita temukan jawabannya dengan mencermati ilustrasi berikut.
☞ Proyeksi Titik pada Bidang

Pada gambar di atas, garis tegak lurus dengan garis . Dengan demikian, titik adalah proyeksi titik pada bidang .
☞ Jarak Titik ke Bidang
Pada gambar di atas, jarak titik ke bidang sama dengan panjang ruas garis .
Hubungan antara Dua Garis
Ada empat hubungan yang mungkin antara dua buah garis.
✿ Dua Garis Berimpit
- Garis dikatakan berimpit dengan garis jika setiap titik pada garis terletak pada garis .
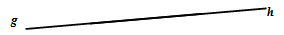
✿ Dua Garis Sejajar
- Garis dikatakan sejajar dengan garis jika kedua garis tersebut tidak mempunyai titik persekutuan dan sebidang.

Nah, untuk menentukan jarak antara dua buah garis sejajar, kalian dapat menggunakan cara seperti ilustrasi berikut.

Pada ilustrasi di atas, jarak antara garis dan sama dengan panjang ruas garis .
✿ Dua Garis Berpotongan
- Garis dan dikatakan berpotongan jika kedua garis tersebut mempunyai tepat satu titik persekutuan dan sebidang.

✿ Dua Garis Bersilangan
- Garis dan dikatakan bersilangan jika kedua garis tersebut tidak mempunyai titik persekutuan dan tidak terletak dalam satu bidang.

Hubungan antara Garis dan Bidang
Hubungan antara garis dan bidang ada tiga macam.
✿ Garis Terletak pada Bidang
- Sebuah garis dikatakan terletak pada bidang jika garis dan bidang tersebut mempunyai dua titik persekutuan.

Pada ilustrasi di atas, garis terletak pada bidang .
✿ Garis Sejajar Bidang
- Sebuah garis dikatakan sejajar dengan bidang jika tidak ada titik persekutuan atau garis tersebut sejajar dengan salah satu garis yang terletak pada bidang tersebut.

Pada ilustrasi di atas, garis sejajar dengan bidang .
Nah, untuk menentukan jarak antara garis dan bidang yang sejajar, kalian dapat menggunakan cara seperti ilustrasi berikut.

Jarak antara garis dan bidang sama dengan panjang ruas garis .
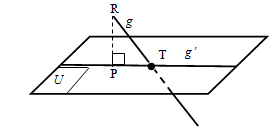
✿ Garis Menembus/Memotong Bidang
- Sebuah garis dikatakan memotong/menembus bidang jika terdapat satu titik persekutuan.

Pada ilustrasi di atas, garis memotong/menembus bidang dengan titik potongnya adalah titik .
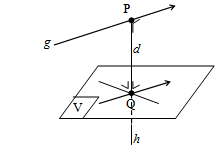
Nah, untuk menentukan proyeksi garis dan besar sudut, kalian dapat menggunakan cara seperti ilustrasi berikut.

Pada ilustrasi di atas, garis tegak lurus dengan bidang . Dengan demikian, proyeksi garis pada bidang adalah garis atau garis . Adapun sudut antara garis dan bidang adalah .
Apakah kalian sudah paham dengan penjelasan di atas?
Masih ada satu hubungan lagi yang perlu kalian pelajari, yaitu hubungan antara dua bidang.
Yuk kita cermati uraian berikut.
Hubungan antara Dua Bidang
Dua buah bidang dapat berimpit, sejajar, atau berpotongan.
✿ Dua Bidang Berimpit
- Dua bidang dikatakan berimpit jika mempunyai tiga titik tidak segaris yang merupakan titik persekutuan.

Pada ilustrasi di atas, bidang berimpit dengan bidang .
✿ Dua Bidang Sejajar
- Dua bidang dikatakan sejajar jika tidak mempunyai titik persekutuan.

Nah, untuk menentukan jarak kedua bidang, kalian dapat menggunakan cara seperti ilustrasi berikut.

Pada ilustrasi di atas, jarak antara bidang dan sama dengan panjang ruas garis , yaitu satuan.
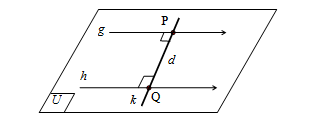
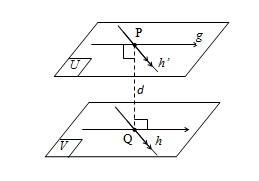
✿ Dua Bidang Berpotongan
- Dua bidang dikatakan berpotongan jika ada tepat satu garis persekutuan.
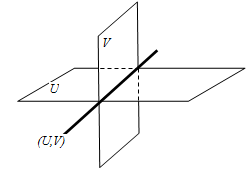
Pada ilustrasi di atas, bidang memotong bidang , dengan garis potongnya adalah .
Agar kalian lebih paham mengenai materi di atas, yuk kita perhatikan contoh berikut.
Contoh
Pada kubus , tentukan
- garis yang sejajar dengan garis FG
- proyeksi garis CE pada bidang ABCD
Penyelesaian:
Perhatikan kubus berikut.

Pada gambar di atas, tampak bahwa
- Garis yang sejajar dengan garis adalah garis , , dan
- Garis tegak lurus bidang , sehingga proyeksi garis pada bidag adalah garis .
Tags:
Matematika